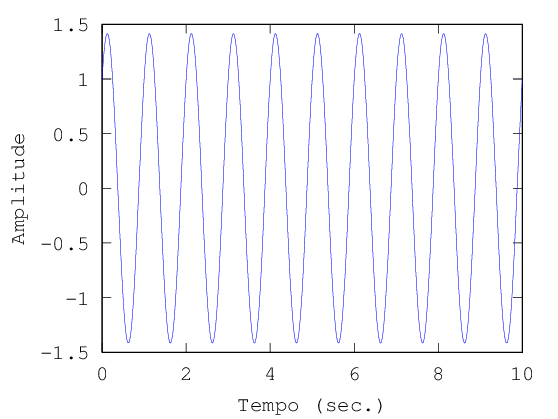
Resposta à condições iniciais

A resposta livre de um sistema de um grau de liberdade sem amortecimento pode ser calculada a partir da solução da equação diferencial ordinária

\[m\ddot{x}(t)+kx(t)=0\]

sendo que \(m\) é a massa do sistema, \(k\) é a rigidez, \(x\) é o deslocamento. A solução é dada por

\[x(t)=x_0\cos{(\omega_n t)}+\frac{v_0}{\omega_n}\sin{(\omega_n t)}\]

E \(x_0\) e \(v_0\) são, respectivamente, o deslocamento e a velocidade no instante de tempo inicial (\(t=0\)). O termo \(\omega_n=\sqrt{\frac{k}{m}}\) é a frequência natural do sistema

m = 1.;
k = 1.;
wn = sqrt(k/m);
x0 = 1;
v0 = 1;

t = linspace(0,10,1000);
x = x0*cos(2*pi*wn*t)+v0/wn*sin(2*pi*wn*t);

plot(t,x)
xlabel('Tempo (sec.)')
ylabel('Amplitude')